Second grade squares
I posed a second-grader the question of what nine squared was. She reasoned that ten squared is 100, and nine times ten is ten less then that, and nine times nine is nine less than that, so the answer is 81. Then I asked her what eight squared was, and she was flummoxed. She saw that it was a similar problem to the one she’d just solved, but wasn’t sure how to apply the analogy.
Here are the pictures that showed her how to figure out the answer. We drew the location of the squares on a multiplication grid:
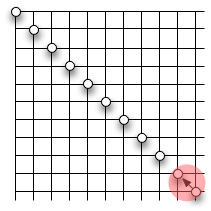
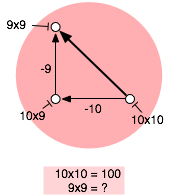
and I introduced the idea of a “solution structure”. A solution structure is a graphical representation of the steps of a solution. This is the section that represents the relation between 92 and 102.
Two problems can have different numbers but the same structure. This is the problem structure for both problems shown together:
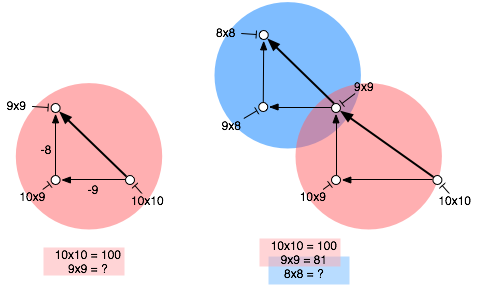
And then she got it.
But this leads to the arithmetic problem of 81 minus 17, which was harder, for this seven-year-old, than 100 minus 10 minus 9. There are several ways to compute the difference between 81 and 17. The hard ways are to count down by 17, or to do two-digit subtraction and carry the one. The easy way is to adjust the problem to 84 minus 20, and count down two tens to 64. But how can you show that 81-17 = 84-20?
Here’s what didn’t work: explain that adding three to both the minuend and the subtrahend leaves the difference unchanged. Seven was too early for something this symbolic. We used a number line instead:
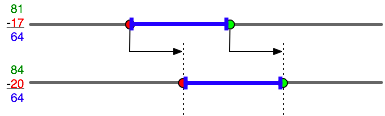
The difference is the blue bar. Moving it on the number line moves its ends by the same amount, without changing the length of the bar itself. Conversely, you can move both ends by the same amount without changing the length of the line between them.
Problem solved.