Adding Fractions
Here’s a picture I drew to explain addition and subtraction of fractions to the sixth-grader:
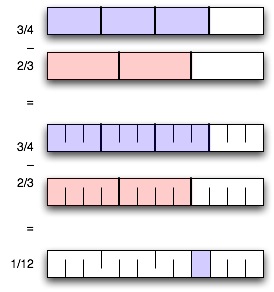
We also ended up using a variant on Euclid’s algorithm for finding the GCD. It uses subtraction instead of division and remainder; it’s in general less efficient, but it’s easier to explain and can be easier to do in your head, when the numbers are small.
Construct a series whose first two terms are the inputs, and then continue as follows: each successive term is the absolute value of the difference between the preceding two terms — that is, simply subtract the smaller from the larger. If you reach one, the GCD is one; if you reach zero, the GCD is the previous term. (Or, you could also let the series peter out to zero, but the way I’ve stated it is simpler in practice.)
-
24 and 16: 24, 16, 8, 8, 0.
-
9 and 7: 7, 9, 2, 7, 5, 3, 2, 1.
-
12 and 9: 12, 9, 3, 6, 3, 3, 0.
-
35 and 28: 35, 28, 7, 21, 14, 7, 7, 0.
An added advantage is that the first step lends itself to an optimization that almost always short-circuits the whole process, at least for sixth-grade math problems. Take the difference of the two inputs and test whether that divides both of them. If it does, that’s the GCD.